Creating Synthetic Data via Neural Placement
Contextual placement using pre-trained vision models
Early on in Bifrost’s journey, we took the simplest approach to create object detection scenarios: composite objects randomly on backgrounds. However, as contextual placement became necessary, the approach didn’t scale.
Why contexual? We need to create specialized samples to reinforce distributions and correlations in synthetic datasets. Object detectors trained on synthetic data, for instance, can fail on objects in rare or unrepresented contexts (referring to the environmental pixels surrounding the object), like aircrafts in grassy fields, or large boats in shipyards instead of on water.
We thus built a smarter, but simple, method of determining suitable placement areas in large images, which we endearingly named Mise en Place.
Embedding image areas into vectors
The early layers in trained convolutional neural networks are powerful feature extractors, even on smaller inputs[1]. We can exploit these layers to project small areas of the image into a feature embedding space, in which the embedding vectors have some notion of vector similarity.
Here’s how it works. We first split the original tile into a grid, feeding each individual cell into the initial layers of a pre-trained network (which collectively act as an encoder) and obtaining an embedding vector for that cell:
This vector acts as a latent representation of the content of the input cell.
We then compute the cosine similarity between each cell’s embedding vector $(v_i)$, and every other vector $(v_j)$, for every $(j \in S \setminus i)$, $$\text{sim}(v_i, v_j) = \frac{v_i \cdot v_j}{\lVert v_i \rVert \lVert v_j \rVert}$$
Why not just compare the images directly?
Evidently, similar cells produce vectors similar to each other. Now, one may wonder, why bother transforming the image cell into a vector? Why not simply calculate the similarity (or difference) of the input cell directly? Here’s the problem.
Say we’re contrasting two cells (X) and (Y) by taking the sum of the absolute differences between corresponding pixel values:
$$\text{dist}(X, Y) = \sum_{i,j} \left\lvert,X_{i,j} - Y_{i,j},\right\rvert$$
For the pairs below, the top pair has a total difference of (951103), and the bottom (490118). What’s happening here?


Let’s look at the top row. The two cells seem visually similar, but the position of the diagonal feature doesn’t line up perfectly. This causes the absolute difference between the two images to be large, showin up as white areas in the difference map.
On the other hand, the bottom pair of cells don’t look similar at all, and ar likely from different areas of the original image. But their difference remains low, since pixel value coincidentally match at the same locations, resulting in a lower difference score.
The usefulness of the neural network her is in its translationally-invariant representation of the features in the image, creating embedding vectors that encode the content of each cell, rather than their literal values.
Selecting matching vectors
Now that we’ve scored our cells, we’ll want to query a single cell, and search for all the similar cells in the image. For instance, we’ve got this snazzy looking cell of… dirt over here.

Since we have this query’s similarity scores for every cell, we can rank the cells, filtering those most similar to it. The naïve approach is to choose the top-(k) similar cells, but the manual task of determining the optimal number of cells remains. An alternative is to let the image speak for itself: we’ll break down the distribution of scores into a Gaussian mixture model[2] and select cells belonging to the highest-scoring cluster.
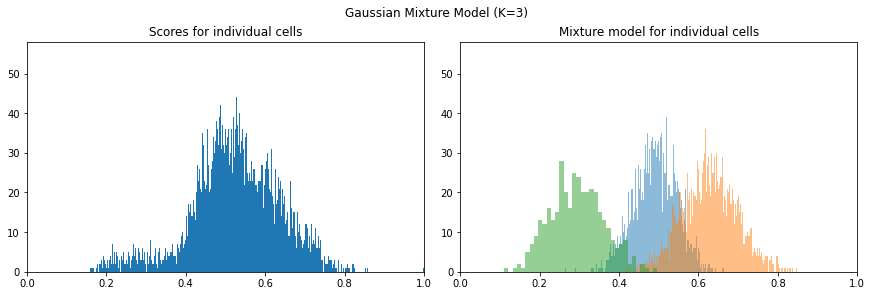


Doing science
We might have managed to produce a visually consistent result, but we’ll also need to design a performance metric, which lets us perform science: tweak parameters and measure how things change. From the final group of similar cells, we can recover a coarse segmentation mask, compared to the original land-cover segmentation mask on the right. Though we’ve managed to match a significant proportion of the cover, we’ve also let too much through.

To quantify our closeness to the original segmentation mask, we’ll employ the Jaccard index[3], or intersection-over-union (IoU):
$$J(y, \hat{y}) = \frac{\lvert y \cap \hat{y} \rvert}{\lvert y \cup \hat{y} \rvert} = 0.447$$
That’s great! Now we’re able to tweak some design choices and observe how close our results are to the ground-truth segmentation.
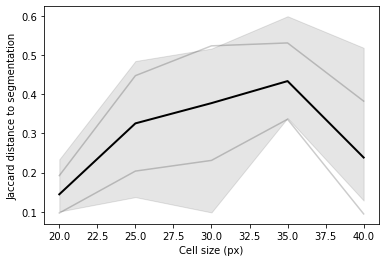
For instance, we can vary the cell size, and track its effect on the Jaccard index. For each cell size, we’d take the average IoU over 5 runs, using a random query cell each time. This hints that the optimal cell size for this particular image is around 35px – if we’re restricting ourselves to a fixed cell size, we can run this experiment over many images and try and determine the best average case.
Conclusion
This was a useful early approach to distribute objects on underrepresented areas. Though this method retains and leverages the raw power of a trained neural network, it’s fast and quick to develop, since no training is involved!
References
- 1.Sergey Zagoruyko, & Nikos Komodakis (2015). Learning to Compare Image Patches via Convolutional Neural Networks. arXiv preprint arXiv: Arxiv-1504.03641. ↩
- 2.Duda, R., & Hart, P. (1973). Pattern classification and scene analysis. (Vol. 3) Wiley New York. ↩
- 3.Jaccard, P. (1912). THE DISTRIBUTION OF THE FLORA IN THE ALPINE ZONE. New Phytologist, 11(2), 37-50. ↩